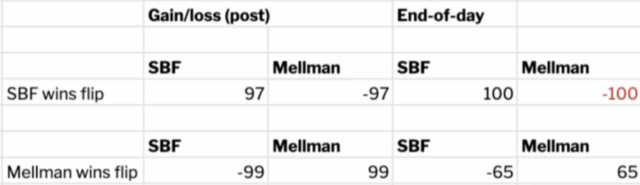
|
虽然，此刻仍然是SBF的期望值更高，但Asher仍然有50/50的机会决定性地赢得赌局：
首先，参与赌局会给Asher带来更大风险的同时也会带来更多的回报：
- 如果他让别的实习生参与，他一定会损失≥33美元
- 如果他参与，他要么损失100美元，要么赚66美元。
这似乎也限制了SBF的上涨空间。由于Asher的损失上限为100美元，因此如果损失97美元，他将无法支付赌注中的余额，这意味着SBF（大概）获利 100 美元，而不是 130 美元。
倾尽所有的赌徒
SBF曾口述了部分赌局的内容，他说：“当你用正确的表达勾起他人的兴趣时，人们会变得如此着迷于免费的美元。”
有评论指出，在这个故事以及其他关于SBF早期交易生涯的轶事中可以看到，SBF擅长计算期望值，善于找到方法来让交易对手感到痛苦，但他不擅长确定交易规模，且他根本就不考虑这个问题。
SBF对所有的交易都采取全力以赴的策略，在他的世界观中，如果你在赌局中存在1%的优势，你应该一次又一次地把你的所有钱都押上，直到你输光为止。
分析指出，作为Jane Street的实习生，你每天有100美元可以下注，你的部分工作就是用这100美元尽可能的多赚钱，但将全部资金（甚至98美元）投注在仅具有1%优势的单一投注上真的是最佳选择吗：
凯利公式指出，在一个期望收益为正的重复性赌局或者重复性投资中，每一期应该下注的最优比例。鉴于实习生的资金为 100 美元，我认为凯利会告诉你最多在这个赌注上投入10美元，98美元太多了。
当我读到这一段的时候，我会感叹Jane Street到底在教那些实习生什么？
但也有分析指出，回想一下2020年，SBF在X（原twitter）上与Matt Hollerbach关于凯利准则争论，SBF称，他的赌金肯定会比“凯利准则计算出的更多”。为什么呢？因为SBF更相信他的效用函数（衡量个人满足度的方式），不像传统模型中通常假定的是对数增长的，效用函数更接近于线性增长。
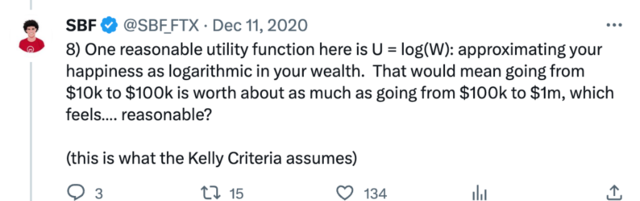
正因这样的心态，SBF更愿意“All in”，以追求更大的回报，因为他相信每一单位的额外收益对他的整体满足度有更大的影响，而不会担心风险。SBF告诉Lewis，他需要“无限资金” 。
但或许正是“无限资金”背后被SBF忽视的“无限风险”最终将他推入深渊。
来源：华尔街见闻 葛佳明 共2页 上一页 [1] [2]
红商网优质内容还将同步分发到公众号、视频号、头条号、西瓜抖音、网易号、搜狐号、企鹅号、百家号、好看视频、新浪微博等国内主力流量平台。
|
